notes

In here are the list of things I did for a particular hour or day. Also included here are the screenshots of games I played, or videos I watched or listened to, or just random things I stumbled upon. I'll occasionally write down what I'm thinking, or things I'm planning to do.

[ 2024-02-14 ]

🕒 15:52

🕒 15:11

🕒 15:10

🕑 14:11

11:52 [link] [context] #math

Aha, I found what I'm looking for:

 (ab)^-1 = (a^-1)(b^-1)

Or not, this only applies to a group with one operation. Actually, an algebraic system with two operations is called a ring, not a group. I'll skip ahead to chapter 17 of the book and see if I can find the relevant theorem I'm looking for. It's funny how I'm just like skimming an API documentation and looking for something I can use to bring my abomination into fruition.

🕚 11:16

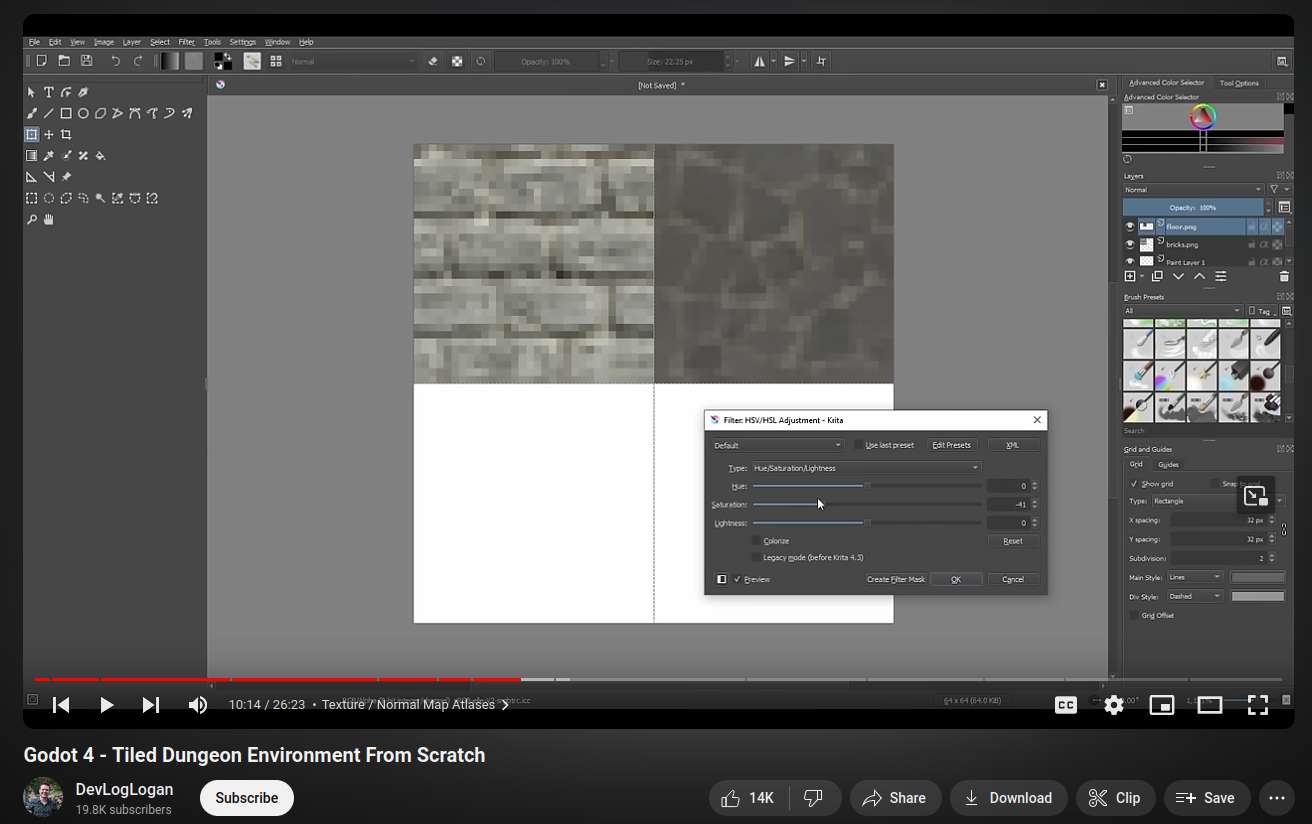
10:46 [link] [context] #math

Now, I'm trying to follow an example of how to get the derivative of 1/x. Once again, whenever I see I fractions, I frequently scratch my head how did the book go from this to that. I should probably learn the basics how to combine fractions together, but I am weirdly fixed on notational purity, so I want to see could I solve this just in terms of exponents.

First, consider the equation:

   1/(x+y) - 1/x
 = 1/(x+y) + -1/x
 = (x+y)^-1 + x^-1

Now, I'm stuck. How do I simplify this? Can I distribute ^-1 inside (x+y)?

 (x+y)^-1 =? (x+y)1^-1

Are these two equal? Nope. I do know that

 x^n = (x^a)(x^b) where n = a+b

So (x+y)^n = ([x+y]^a)([x+y]^b)

Nope, it's even more complicated now, I've further strayed away from the light, the opposite of simplifying.

Oh well, I think I'll read the book of abstract algebra first.

🕙 10:04

🕙 10:03

🕓 04:10

🕒 03:52

🕒 03:07

🕑 02:46